Research

The Hybrid Labs Project
PI Julia Gouvea and Aditi Wagh, funded by the Davis Foundation

The Hybrid Labs project is developing undergraduate biology laboratories that couple computational modeling and experimentation and training graduate student TAs in new pedagogy. Research in the project will study both undergraduate students' and graduate TA's learning of practices in science and approaches to teaching.

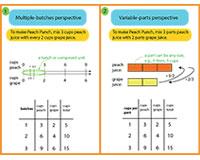
Investigating Proportional Relationships from Two Perspectives (InPReP2)
Professor Andrew Izsák with Co-Investigators Sybilla Beckmann and Laine Bradshaw at the University of Georgia

The InPReP2 project is investigating how future middle and secondary school mathematics teachers develop quantitative understandings of multiplication, division, and fractions that they can then use to build understandings of ratios and proportional relationships and applications to linear equations and statistical samples. The study focuses on two perspectives on ratios and proportional relationships, one of which has been largely overlooked in past mathematics education research. The two perspectives are developed in mathematics content courses that future service teachers take as part of their preparation programs. The project examines the future teachers' reasoning as they participate in these courses and compares their facility with proportional relationships to that of future teachers in a "business as usual" content course at a second university.

Focusing on Multiplicative Foundations to Enhance Access to Calculus  
Andrew Izsák, funded by the Spencer Foundation

This project addresses two long-standing challenges for mathematics education. The first challenge is broadening access to calculus, and the second challenge is responding to decades of research reporting college students’ difficulties with multiplication and division when asked to model relationships between quantities (e.g., lengths, volumes, speeds). The project is investigating the conjecture that ways students perceive when and what to multiply, and what quantities are then produced, may limit success they experience with calculus. The project is conducting clinical interviews with university STEM students using tasks that provide opportunities to reason about integrals with bounds in the context of physical situations. The project is focused on integration because there has been much less research on students’ understanding of integration than on differentiation, and because the research on integration that does exist hints at college students’ challenges modeling situations with multiplication.

Community Tech Press 
Kristen Wendell and Greses Pérez, in collaboration with Chelsea Andrews at the Tufts CEEO. Funded by the National Science Foundation

The Community Tech Press project is a curriculum development and research project with Somerville Public Schools. While many existing middle-school engineering curricula emphasize creating an optimal solution to an engineering design problem for a client or user, this project takes a civic-oriented approach. Students engage in engineering to critically evaluate climate technologies affecting their local community. Then, they construct and convey messages about climate tech for an audience of family members, community groups, or civic leaders. The research team is exploring how this critical technology journalism approach influences engineering learning among 6th-grade youth, including students from multilingual families.

Design Talks 
Kristen Wendell in collaboration with Jessica Watkins at Vanderbilt University and Chelsea Andrews at the Tufts CEEO. Funded by the National Science Foundation

The Design Talks project is exploring whole-class engineering design discussions that teachers facilitate with pre-college students. Working closely with elementary school teachers, the Design Talks research team studies how whole-class conversations can help students share and listen to thinking about engineering design problems and solutions. One focus of the project is to foster student reasoning about the social, historical, and political contexts of design problems and solutions.

Hip Hop Making Spaces
Tufts PI Brian Gravel, funded by NSF

This collaboration between Drexel, Olin College of Engineering, and TERC explore the relationships between the five elements of hip hop and computational making practices in STEM. Through the design of workshops that draw from hip hop principles, culturally sustaining pedagogy, and aspects of STEM-rich making, we explore youth identities and STEM learning.

Early Childhood and Elementary Mathematics Research 
Bárbara M. Brizuela

Professor Brizuela studies children’s learning of elementary mathematics including mathematical representations, number, and early algebra. In the latter her research has ranged from developing learning trajectories and progressions for algebraic concepts, such as variables and functions, to understanding how the distribution of mathematical authority shapes students’ engagement.

Exploring K-2 Children Understandings of Visual Representations in Algebraic Reasoning  
PI Bárbara M. Brizuela, co-PI Maria Blanton at TERC, and Research Associate Susanne Strachota, funded by the NSF

This project involves collecting data from K-2 students in classrooms and interviews to understand their use of the visual representations, such as function tables and Cartesian coordinate graphs. The aim is to develop learning trajectories as cognitive models of how children in grades K–2 use visual representations to reason algebraically.

ConnecTions in the Making: Integrating Science and Engineering to Design Community Solutions

Kristen Wendell, in collaboration with Dr. Tejaswini Dalvi at UMass Boston and local teachers and administrators, the ConnecTions project supports teachers in learning to integrate engineering design with science inquiry in elementary classrooms, in a context of solving local problems that matter in their students' communities. Some of those problems have been identified in collaboration with scientists and engineers from Boston's MBTA transit system, the "T." The project team has co-developed six new curriculum units with collaborating educators and is conducting classroom studies on student reasoning and practice as the units are enacted.

Re-Making STEM 
Tufts PI Brian Gravel, James Adler, and Tim Atherton, funded by NSF

Re-Making STEM is a professional development collaboration between Tufts University, TERC, Olin College of Engineering, Malden Public Schools, and Cambridge Public schools. Together, researchers and teachers are exploring the idea of "computational making" within STEM disciplines to examine how computational thinking, computational tools, and multiple ways of knowing come together in "making" to provide powerful opportunities for learning.

Dynamics of Learners' Engagement and Persistence in Science 
David Hammer

Dynamics of Learners' Engagement and Persistence in Science is funded by the Gordon and Betty Moore Foundation. The project looks across educational experiences from elementary school to university to find examples of students' engagement in science, in particular moments, lasting for days, or even personal transformations over a semester. Within each of these, we are studying what contributes to that engagement—how it begins, how it sustains.